Evolution chart dari Gell-Mann:
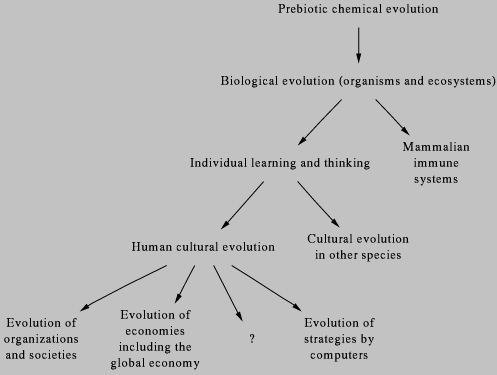
Evolution chart dari Gell-Mann:

Waktu Feynman bertanya ke Schwarz (Berapa dimensi kamu hari ini?), sebenernya dia nggak ngece-ngece amat. Emang bawaannya aja. Tapi setidaknya, dia termasuk minoritas fisikawan besar — bersama Murray Gell-Mann yang mau hadir di seminar Schwarz itu. Dan waktu itu pun sudah jarang Gell-Mann dan Feynman bisa hadir dalam sebuah acara bersama2, nerusin acara cela2an berdua yang beberapa tahun sebelumnya sudah jadi kelaziman (sambil masuk ke acara Schwarz itu, Gell-Mann menyebut nama kota Montreal dengan lafal yang tepat seperti penduduk Montreal, i.e. Mon-ray-al, tapi Feynman berkeras belum pernah mendengar nama kota kayak gitu). OK. aku emang lagi doyan berseliweran kalo nulis weblog. Sorry.

Jadi itu beberapa tahun sebelum Schwarz ngetop di luar kelompok fisikawan yang terbatas itu. Feynman sendiri termasuk yang paling doyan main2 dengan spekulasi fisika dan matematika. Waktu di SMA, dia belajar kalkulus. Menghitung turunan pertama sebuah fungsi, turunan kedua, turunan ke n, dan mengambil suatu pola. Terus dia mikir: gimana kalau ada turunan kesetengah? Atau semacam itu. Jadi sesuatu yang mentransformasi sebuah fungsi, dan kalau ditransformasikan lagi menjadi turunan pertama dari fungsi itu. Ide itu baru dikerjakan waktu Feynman benar-benar menguasai kalkulus di universitas. Dan benar-benar terpakai waktu proyek Los Alamos.
Soal dimensi sendiri sering jadi bahan permainan Feynman. Apa yang terjadi kalau dunia ini cuma dua dimensi? Dia turunkan formula2 fisika ke ruang dua dimensi, dan mendapati bahwa spektrum atom2 itu jadi menarik sekali. Terus gimana kalau … bukan cuman ruang yang dipakai bermain … tapi juga waktu. Gimana kalau waktu bukan cuma 1 dimensi, tapi juga dua dimensi. Waktu bukan cuma depan dan belakang (soal waktu maju mundur, sila baca catatan-catatan sepanjang awal 2001), tapi ada semacam kiri dan kanan juga :). Apa yang terjadi pada hukum fisika?
Lalu Feynman berkisah tentang si sohibnya yang dikagumi tapi suka diajak bertengkar itu, tanpa menyebut nama. “Ada seseorang yang pernah mencoba berpikir: apa jadinya kalau partikel di dunia ini cuman tiga. Eh, terjadi inkonsistensi, misalnya pada K-meson. Jadi dia berpikir: apa jadinya kalau ternyata angka muatan itu tidak harus bilangan bulat?” Dan tepat itu lah yang bikin Gell-Mann jadi ilmuwan kelas dunia: kuark.
Leonard Mlodinow, waktu masih ragu memulai kerja sama dengan Schwarz, menanyakan ke Feynman: “Gimana pendapat Anda kalau saya memulai proyek yang kata orang omong kosong?”
Feynman menjawab: “Satu syaratnya.”
Mlodinow penasaran: “Apa itu?”
Feynman: “Bahwa menurut kamu itu bukan omong kosong.”
Dalam cerita ini sang profesor bermain roulette bersama asistennya, Cindy. Atau nama lain, terserahlah, aku juga nggak ingat. Cindy memegang pistol kuno berisi setengah penuh, bertugas menembakkan peluru panas tepat ke kepala Profesor. Profesor berwajah tenang dan penuh percaya diri, sementara Cindy berwajah tegang dan sedikit pucat.
“Dor,” suara bising mengiringi letupan pistol tanpa peredam suara itu.
Dengan tegang Cindy menatap Profesor yang masih tersenyum. “Teruskan,” perintah Profesor. Lebih tegang, Cindy memutar kantong peluru, lalu melakukan tembakan kedua. Profesor masih tersenyum. Dan dengan ketegangan memuncak, Cindy melakukan tembakan ketiga. Teror yang amat sangat menyelimuti ruangan, ketika peluru menghancurkan kepala Profesor.
Adegan selanjutnya tidak perlu diulas, karena website ini terbuka untuk segala umur. Cindy jatuh terduduk, nyaris pingsan. Bagaimana pun, ia hanya menjalankan perintah.
Tapi itu versi Cindy.

Sekarang kita dengarkan versi Profesor.
“Teruskan,” perintah Profesor setelah peluru pertama. Cindy menembak. Masih kosong. Tidak tega Profesor melihat ketegangan yang memuncak di wajah Cindy. Ia memberikan isyarat mata untuk tembakan ketiga. Masih kosong juga. “Ayo cepat kita selesaikan,” kata Profesor. Cindy membidikkan pistol. Tembakan berikutnya masih kosong. Juga berikutnya. Juga berikutnya. Sampai tembakan ke seratus, Profesor memberi tanda berhenti. Lalu dengan riang ia berteriak, “Eksperimen berhasil!”
Dalam proposisi ini, pengamat yang berbeda bisa mengamati hasil eksperimen secara berbeda. Pada tembakan pertama, probabilitas bahwa peluru akan tertembakkan adalah 50%. Kans profesor untuk hidup tinggal 50%. Dua tembakan memberi kans 25%. Tiga tembakan, 13%. Bagi Cindy, Profesor sudah cukup beruntung bahwa ia mati setelah tembakan ketiga (probabilitas hidup tinggal 13%). Tapi bagi Profesor, kalau ia mati, ia tidak bisa memberikan hasil pengamatan. Jadi bagi versi Profesor hidup, sampai tembakan ke-100 pun ia tidak bisa mati.
Dan kalau kenyataan bagi para pengamat itu berbeda, apa itu artinya semesta paralel jadi valid? Atau tanpa jadi paralel pun, multi-realitas bisa terjadi? Versi terakhir ini lebih menarik.
Apa bedanya?
Kita kembali ke eksperimen celah ganda (yang banyak ditulis di web ini tahun 2000-2001). Saat elektron tunggal ditembakkan di depan celah ganda, ia berinteraksi dan membentuk pola interferensi. Tapi interaksi dengan siapa? Barangkali waktu elektron ditembakkan, masing2 celah menerima satu elektron dalam realitas yang terpisah. Realitas terpisah, tapi masih bertetangga, dan bisa menyatu lagi.
Konsep multi-realitas juga bisa jadi jawaban yang cepat (dan dangkal) untuk menjawab pertanyaan khas zaman Interpretasi Kopenhagen: siapa sang pengamat? Bagaimana kalau ada banyak pengamat? Realitas menjadi lebih tergantung lagi pada pengamat. Di salah satu frame realitas yang lain, bukan manusia yang jadi pemenang dalam evolusi makhluk hidup. Dalam frame yang lain lagi, bumi tidak pernah terbentuk.
Esse es percippi, kata Berkeley. Mudah2an aku nggak salah eja lagi. Mungkin memang nggak masuk akal dan menyebalkan. Tapi, kayak yang pernah aku tulis, aku punya pertanyaan dari waktu aku berumur sekitar 5 tahun, dan belum terjawab juga. Dan barangkali cerita yang satu ini bisa mulai membuka jawaban.
Sumpah, aku bukan fans Richard Dawkins, biarpun kayaknya nama ini udah mulai sering ditulis di site ini. Aku cuman rada tertarik baca ulasannya dia, tentu tentang genetika, tapi pakai Hk Moore. Kita tahu, Moore bikin estimasi eksponensial itu untuk chip, untuk transistor, bukan untuk genetika. Tapi yang dibahas Dawkins itu soal pemetaan DNA. Dan artinya soal IT. Dan artinya soal prosesor lagi, chip lagi.
Dawkins mengambil data dari Jonathan Hodgkins, tentang biaya yang dikeluarkan untuk memetakan DNA, sejak 1965. 1965, wow. Waktu itu penelitian DNA masih sedemikian mahalnya, sehingga perlu £1000 per huruf untuk memetakan RNA ribosome suatu bakteri. Belum DNA sih, masih RNA. Tahun 1975, pemetaan DNA virus X.174 membutuhkan £10 per huruf. Tahun 1985 nggak ada data. Tahun 1995, perlu £10 per huruf untuk memetakan DNA sebuah nematoda kecil. Pada proyek GENOME manusia di tahun 2000, diperlukan biaya £0.1 per huruf. Dari situ, Dawkins menyusun plot, plus ekstrapolasi, sambil menyadari bahwa ini tidak terlalu serius. Sampel 4 data tentu sama sekali tidak ilmiah.
Hasilnya dibikin nggak serius juga, maunya. Dengan £1000, kita bisa memetakan seluruh DNA virus Herpes di tahun 2020. Tahun 2030, uang yang sama bisa dipakai memetakan DNA lalat buah. Dan tahun 2040, uang yang sama bisa memetakan DNA mamalia, termasuk manusia. Di tahun 2050? Semua manusia bisa memetakan DNA masing-masing cukup dengan £100.
Wow, dengan data kayak gitu, cukup main2 DNA untuk mengerti seluruh sejarah evolusi, sejarah peradaban dan migrasi manusia, silsilah manusia dari zaman prasejarah. Kalau sekarang kita periksa paru2 dengan Röntgen, nanti kita bisa sekalian tes DNA, dan para dokter bisa mengobati kita bukan berdasar gejala rata2 manusia, tapi persis sesuai karakteristik fisik kita. Tapi data yang sama bisa dipakai untuk menerima atau menolak kita bekerja, bisa dibajak perusahaan asuransi, pemerintah, militer, dan sebagainya.
Jangan lupa, bermain2 dengan DNA hewan, kita bisa menciptakan kembali spesies yang punah.
Tapi, kayak Moore juga selalu bilang, ekstrapolasi eksponensial selalu berakhir di titik jenuh. Akankah titik jenuh itu tercapai sebelum impian liar Dawkins terjadi?
Any universe simple enough to be understood is too simple to produce a mind able to understand it.
(Astrophysicist John Barrow of Cambridge, quoted in The Wall Street Journal)
Nigel Calder menuding terang-terangan: gambaran Einstein di Time sebagai man of the century itu menyesatkan dan memalukan. Einstein digambarkan sebagai orang tua yang ramah, berambut kusut penuh uban, berbaju lusuh sekenanya. Padahal sang fisikawan yang menggoncangkan dunia hampir 100 tahun yang lalu itu, dan goncangannya masih terasa sekarang, adalah seorang pemuda, tegap, sok tahu, rada congkak. Yup, Einstein muda lah yang dalam satu tahun mempelopori fisika kuantum (dengan efek fotoelektrik), relativitas (yang disusul dengan teori gravitasi baru), sampai gerak Brown.
Tentu tidak ada yang salah dengan bertambah usia, asal kita tidak menjadi tua. Menjadi tua, pikiran kita dihantui oleh pengalaman yang terus bertambah, pengetahuan yang bertambah rumit bercecabang, sehingga hilanglah keberanian meneriakkan pembaharuan dengan lantang, lancang, dan sok tahu, dan hilanglah peluang untuk membuat revolusi baru.
Einstein tua adalah seorang tua. Bermusuhan dengan teori kuantum. Bikin konstanta kosmologi yang membuat orang mengabaikan fakta semesta mengembang. Dan cuma jadi dewa penjawab yang serba bijak, bukan jadi pembaharu lagi.
Juga Newton. Si anak durhaka yang lekas jadi tua. Newton, siapa yang pernah mau dengar omongan pemuda tanggung itu, yang nggak pernah jelas apa yang jadi fokusnya? Tapi ada yang mau dengar. Isaac Barrow, orang tua yang benar-benar bijak, yang benar-benar mau meninggalkan posisi keprofesoran mewahnya di Cambridge untuk memberi tempat bagi si pemuda tanggung yang baru beberapa bulan lulus, dan memungkinkannya untuk membuat revolusi fisika (mekanika, optika, kalkulus, gravitasi, dll). Sayangnya Newton tua tidak mengikuti teladan yang baik ini :).
Jurnal ini bukan tipe jurnal yang bisa nulis kalimat semacam “Jadi orang-orang tua, kalau kalian benar-benar punya kebijaksanaan, mundurlah dan beri kesempatan pada orang-orang muda.” Tidak menarik untuk memilih jalan hidup yang menunggu kesempatan yang diberikan orang. Tidak harus jadi Newton muda. Jadilah Einstein muda yang bisa bikin revolusi biarpun dari bagian dunia yang sunyi dan nyaris tak terdengar. Maju tanpa menunggu.
Dan kelak mundurlah tanpa menunggu.
Tintin au Pays des Savants, ISBN 287424015X. Berapa persen dari kisah petualangan Tintin yang berkaitan dengan para ilmuwan? Cukup besar, khususnya kalau kita ingat bahwa orang ketiga (atau makhluk hidup keempat) terpenting adalah Profesor Cuthbert Calculus (atau dalam versi Herge yang asli dalam bahasa Belgia-Perancis bernama Tryphon Tournesol), yang menemukan berbagai hal, dari roket yang bisa menjangkau dan mendarat di bulan (lengkap dengan sistem kontrol dan sistem tenaga dan modul kendaraan di bulannya), mesin perusak dengan ultrasonik, kapal selam mini, pil anti kecanduan alkohol, obat anti racun N14, dan masih banyak lagi. Selain Calculus, Tintin juga bertemu dengan astronom yang menemukan jenis logam baru, antropolog yang sibuk mendalami budaya Mesir atau Peru, farmakolog Cina yang bisa menyembuhkan kegilaan akibat racun, dan tentu komunikator dengan UFO yang ditemui Tintin setelah mengunjungi Jakarta.

Buku ini memaparkan berbagai jenis ilmu, yang sudah terpecahkan maupun yang belum terselesaikan, yang pernah disinggung atau ditohok dalam komik-komik Tintin. Biarpun tidak ada tulisan Herge di dalamnya (selain komik Tintin-nya sendiri), buku ini bakal jadi bacaan yang menarik buat fanatikus Tintin.
Mais si, ici on parle français.
Yang ini kisah nyata dari Ukraina, diceritakan oleh fisikawan Rusia yang melarikan diri ke US — George Gamow.
Igor Tamm, seorang profesor, hidup di Odessa saat Tentara Merah mulai menguasai Ukraina. Tentara Merah bukannya masuk tanpa perlawanan. Gerilyawan tradisional kossak terus menerus berkelana melakukan gangguan terhadap mereka.

Suatu saat, Tamm mengunjungi desa tetangga, membawa setengah lusin sendok perak, untuk ditukar ayam. Karena pakaiannya masih berbau kota, Tamm ditangkap gerilyawan, dan dibawa ke pimpinan gerombolan: seorang tinggi besar brewok berjanggut lebat dengan topi bulu hitam dan senapan mesin tergantung di dadanya.
“Kamu komunis sialan, mengacaukan tanah air kami Ukraina. Kamu harus mati!” teriak si pimpinan.
“Bukan,” sesak Tamm, “Saya profesor di Universitas Odessa dan cuma cari bakan makanan di sini.”
“Bohong! Profesor apaan!”
“Saya mengajar matematika.”

“Matematika!” teriak si ataman. “Kalau gitu, coba turunkan perkiraan error yang terjadi kalau kita memotong deret MacLaurin pada suku ke n. Kalau bisa, Anda bebas. Kalau gagal, mati.”
Sulit Tamm mempercayai telinganya. Itu pertanyaan salah satu cabang matematika tingkat lanjut. Sambil bergetar di bawah todongan senjata, Tamm mulai menulis, dan memberikan hasilnya pada si ataman.
“Wah betul,” kata si boss itu melunak, “Anda memang profesor. Pulanglah.”

Tamm hidup cukup lama, sampai memenangkan Nobel Fisika tahun 1958. Tapi siapa si boss gerombolan itu? Apa dia akhirnya terbunuh dalam deretan perang dan revolusi di Rusia, atau dia juga mengajar matematika lanjut di salah satu universitas di Ukraina? … :)
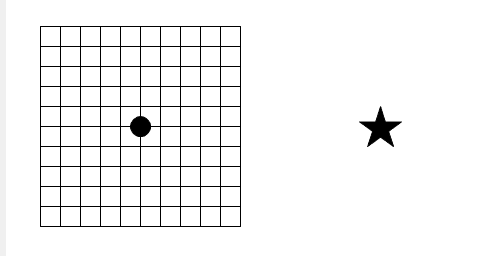
Pernah dengar yang namanya titik buta? Coba lihat gambar di atas ini. Sekarang tutup mata kiri, dan lihat baik-baik titik besar di tengah jaring itu. Pada jarak tertentu dari layar, kita bisa membuat bintang di kanan itu menghilang. Coba mau mundur pada jarak sekitar 10-15 cm, dengan terus melihat ke titik besar. Bintang bisa menghilang? Sulapan? Bukan. Itu daerah yang namanya titik buta.
Sekarang, tutup mata kanan. Eh, buka dulu mata kirinya. Ntar bobo donk. Dengan mata kanan tertutup, sekarang lihat gambar bintang, dan mau mundur sampai titik di kiri itu hilang, masuk ke titik buta. Hilang? Bagus. Tapi coba lihat jaring kotak-kotak kita. Apa ada garis yang hilang? Tidak ada? Kok bisa titiknya hilang tapi garis di sekitarnya tidak hilang? Sulapan?
Nanya melulu. Garis itu ada, karena sebagian jaring ada di luar titik buta, dan otak mengamatinya sebagai jaring kotak-kotak. Ada bagian yang tak terlihat sebenarnya, waktu titik hitam itu menghilang. Tapi otak kita menambahinya. Yup, otak bisa mengisi kenyataan yang kita lihat dengan yang dia pikir seharusnya ada di situ.
Jadi, kalau lain kali melihat sesuatu yang ajaib atau tidak ajaib, coba tanyai dulu si otak: itu benar2 teramati oleh mata atau diciptakan otak seolah2 terlihat ada di sana?
Kemaren aku melupakan John Dalton. Itu salah satu ilmuwan dalam barisan penemu atom, kalau masih inget. Aku sendiri udah lupa — huh. Orang sering menyebut penyakit buta warna sebagai daltonian. Dan Mister Dalton ternyata penderia daltonian. Bukan kebetulan ;), memang nama daltonian diambil dari nama John Dalton. Dalton bukan saja menderita buta warna, tapi juga menyadari bahwa ia buta warna, dan bisa menganalisis bentuk kebutawarnaannya itu. Tentu melalui selang waktu yang panjang.
Dalton tadinya cuma terganggu sama sistem penamaan warna. Kenapa ada warna merah, ungu, biru, hijau, kelabu. Ada warna yang mirip tapi harus punya nama berbeda. Sementara warna lain yang kontras justru memiliki nama yang sama. Tapi dia tidak protes. Kenapa harus protes? Bahasa kan tergantung sejarah juga, bukan soal subyektivitas masa kini. Tapi dia mulai terganggu bahwa warna yang bernama merah itu berbeda di siang hari dan di malam hari. Waktu dia iseng membahas soal itu, dia kaget bahwa orang lain tidak mengamati hal yang sama. Tak seorang pun. Jadi dia terpaksa mengambil kesimpulan logis bahwa pengamatan matanya memang salah. Sebagai ilmuwan dia mengutak atik, di sisi mana dia salah melihat. Di sisi warna merah, tentu. Coba lihat kurva yang kemarin. Apa yang terjadi kalau receptor merah tidak berfungsi. Atau kalau receptor merah memiliki frekuensi kepekaan mendekati hijau atau malahan biru ;).
Dalton mengambil hipotesis bahwa barangkali ada bagian dari retinanya atau bagian apalah di dalam matanya yang tercemar warna biru. Jadi cahaya merah tersaring hilang. Dia lalu menulis wasiat, minta agar matanya diambil dan dibedah untuk diteliti saat ia sudah meninggal.
Wasiat itu dilaksanakan. Tapi tentu saja tidak ditemukan “filter” apa pun di mata ilmuwan itu. Baru beberapa tahun kemudian kita mengerti tentang receptor di retina, dan hal-hal lainnya itu :).
© 2026 Kuncoro++
Theme by Anders Noren — Up ↑