ToE: Exceptionally Simple

Beberapa blog fisikawan sempat ikut teragregasi di Amigos. Tak lagi: bosan dengan flame war dan politik di antara mereka. Kadang saja masih kukunjungi. War akhir tahun lalu menyangkut sebuah preprint yang tersimpan di arxiv, tulisan Garrett Lisi, berjudul An Exceptionally Simple Theory of Everything. Hah? ToE bisa ‘exceptionally simple’? Tentu saja pendukung teori string berang, sementara kelompok Perimeter memberikan dukungan. Terjadi perang yang tak terlalu ilmiah :(.

Tapi Science & Vie bulan ini justru menjadikan paper Lisi sebagai topik utama: “Théorie du tout, Enfin! Un physicien aurait trouvé la pièce manquante.” Pakai tanda seru gitu. Dan pakai ‘missing piece’ kayak makalah2 kuno tentang evolusi (sekarang sudah terpecahkan –red). Terpaksa prep Lisi yang belum selesai dibaca itu dibuka lagi. Tapi, sebelum salah sangka, judul prep ini memang disengaja agak memelesetkan. Arti harfiahnya memang percobaan menyusun ToE tanpa sesuatu yang rumit seperti supersimetri dan dimensi ekstra. Tapi yang juga (sebenarnya) dimaksudkan adalah bahwa struktur yang digunakan dalam prep ini, yaitu E8, merupakan exceptional simple group. Ini adalah struktur aljabar temuan matematikawan Norwegia Sophus Lie. Simple secara matematis berarti bahwa group ini tidak memiliki jenis struktur internal tertentu, dan exceptional hanya berarti bahwa group ini termasuk dalam sejumlah kecil simple Lie group yang tidak termasuk ke kelompok besar keluarga simple group, di mana tak terhingga anggota lainnya berada. Pelesetan ini, dan kehebohan itu, rupanya berhasil menarik media. Walaupun beberapa pendukung Lisi (yang tentu tidak harus 100% setuju paparan ini) menyatakan bahwa diskusi ke khalayak sebaiknya menunggu hingga prep ini benar2 telah diulas para pakar, setidaknya 1 tahun; media sudah mulai berlomba menyampaikan ulasan.

Kembali ke prep. Abstraknya singkat.

All fields of the standard model and gravity are unified as an E8 principal bundle connection. A non-compact real form of the E8 Lie algebra has G2 and F4 subalgebras which break down to strong su(3), electroweak su(2) x u(1), gravitational so(3,1), the frame-Higgs, and three generations of fermions related by triality. The interactions and dynamics of these 1-form and Grassmann valued parts of an E8 superconnection are described by the curvature and action over a four dimensional base manifold.

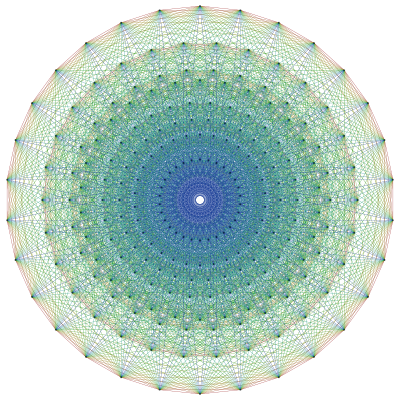
Yummie. Aku bacain paper ini sekitar jam 3 pagi. Mm, harus cerita dari mana ya? Haha. Tapi yang jelas, memang ini masih jauh dari teori lengkap, tak seperti yang dibilang Science & Vie. Huh, dasar media. Eh, nggak dink. Masih jauh lebih cerdas dari detikcom misalnya :). Apa ya misalnya. Di bagian mana sih di paper ini formula2 itu dikuantumkan? Atau memang nggak perlu? Jadi bagaimana mengunifikasikan relativitas dengan mekanika kuantum kalau formulanya belum dikuantumkan? Ah, andai aku jadi matematikawan mendadak untuk memahami hal sederhana ini.

Sementara itu, kalau berminat, coba kita blogwalking tentang tema ini: Sean Caroll, Peter Woit, Jacques Distler, Sabine Hossenfelder. Ada lagi? OK, aku terusin baca dulu …