Novotel, mendekati tengah malam. Pak Rahman masuk lagi ke ruang berlantai kayu itu. Sisa asap Dji Sam Soe ikut terbawa dari beranda masuk ruangan.
“Inget nggak, cara menghitung jarak antara dua koordinat?“
Sebuah bola biru maya segera tergambar di dalam ruangan, lengkap dengan garis2 lintang dan bujur. Dua titik oranye tampil pada posisi sekitar Tokyo dan Mekkah. Sebuah garis ditarik dari Tokyo ke Mekkah, tetapi bukan ke arah barat agak selatan, melainkan justru barat agak utara. Hmmm. Jangan tertipu.
“Kalau jarak dekat sih bisa dengan Pythagoras. Tetapi kalau jauh, kita harus memperhitungkan ..“
“Iya, lengkungan buminya harus dihitung,” tukas Pak Rahman.
“Bukan saja lengkungan. Tapi kebulatan. Arah titik terdekatnya pun belum tentu arah yang sama dengan peta segiempat.“
“Ya sudah. Jadi gimana cara hitungnya?“
Bola maya di tengah ruangan sudah melenyap entah sejak kapan. Aku nggak punya tools selain MS Office di notebook tanpa Internet, yang sedang dipakai mengamati komposisi content di bisnis mobile. “Coba pakai Excel deh,” kataku ngasal. Berorientasi alat, bukan konsep.
“Cobalah.“
Tapi nggak lama, Excel harus ditinggalkan. Yang mulai bermain adalah dua pensil dan bloknot kecil yang semuanya berlogo Novotel. Dua pensil, soalnya sekalian aku pakai untuk membuat simulai visual dari dua koordinat. Obviously, yang harus dicari hanyalah sudut yang dibentuk antara dua koordinat itu melalui pusat bumi. Dan karena tidak ada Internet, aku akan mengasumsikan bumi itu bulat sempurna, seolah jarak utara selatan sama dengan jarak barat timur (hah, ada jarak barat-timur?).
Waktu perhitungan dikoreksi dua kali, Pak Rahman memutuskan merenungi hal lain. Masih dengan sweater ciri khasnya, Mr Workaholic ini tertidur. Aku mendapati bahwa perhitungan kali ini menemui titik terang. Tapi perlu verifikasi. Trus, Excel hidup lagi, dan formula dimasukkan. Grafik dibuat. Ah, sesuai dengan simulasi dua pensil tadi. Ini hasilnya:
Kalau tidak ada mode grafis: cos δ =cos λ1⋅cos β1⋅cos λ2⋅cos β2 + cos λ1⋅sin β1⋅cos λ2⋅sin β2 + sin λ1⋅sin λ2, dengan (λ1,β1) dan (λ2,β2) menunjukkan pasangan lintang dan bujur dua titik, dan δ sudut antara dua titik itu. Lintang utara positif, lintang selatan negatif. Bujur timur positif, bujur barat negatif. Jika δ sudah dalam radian, tinggal mengalikan dengan jejari bumi R untuk menghitung jarak antara dua titik.
Tentu kemudian harus disempurnakan dengan memasukkan variasi R terhadap lintang. Dan ketinggian, kalau diperlukan. Dih. Ntar aja kalau ada Internet.

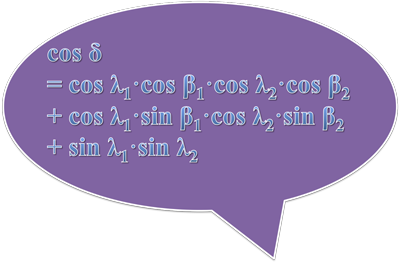

Ya… jadi ingat masa-masa SMA dulu .. ;D
>mas….. aq punya pertanyaan nich.
>kalau hubungan letak geografis dengan jarak gimana yapz????????????
>contoh nya: misalkan bandung letaknya di 153°56″25′
>truzzz jakarta ada di posisi 225°87″99′.
>trus aq mau tau jarak antara jakarta dengan
>bandung berapa???? bila dilihat dari letak
>geografisnya itu loh.thanxs y sebelumnya. kalau bisa mohon di
bantu.penting
aq dah baca tentang apa yang ditulis tentang jarak antara dua titik. tapi kok aq masih belum ngerti yupz…..
he3.kalau bisa tolong disertai dengan contoh dari pertanyaan q di atas ya….thanks so much