Pleumeur-Bodou katanya terpilih dalam proyek Telstar akibat letaknya yang dekat pantai Atlantik dan lingkungannya yang tenang, mendukung kejernihan transmisi yang waktu itu sangat peka gangguan.
Sberapa tahun lalu aku sama beberapa cs berkelana di sekitar pantai Armorik sekitaran kampungnya Asterix, buat mencapai Pleumeur-Bodou. Sopirnya gantian, dan kayak biasa aku jadi navigator. Jalanan dikelilingi tebing berwarna coklat cantik. Dan bahkan sampai titik terdekat, kosmopolis bulat raksasa itu nggak pernah kelihatan. Baru di atas jam 1700 kubah raksasa itu tampak. Kayak bulan purnama yang terbit terlalu dekat. Planetariumnya tutup di musim itu. Tapi museumnya bisa dilihat.
Meneruskan pengelanaan jalan kaki, ternyata kampungnya Asterix juga hanya beberapa puluh meter dari situ, ditata sesuai aslinya, dengan atap jerami. Nggak ada patung Asterix, soalnya ini bukan taman ria. Sayangnya nggak ada menhir Obelix juga. Konon dibawa ke Roma semua buat menghancurkan mata uang Romawi dan bikin Caesar jadi senewen.
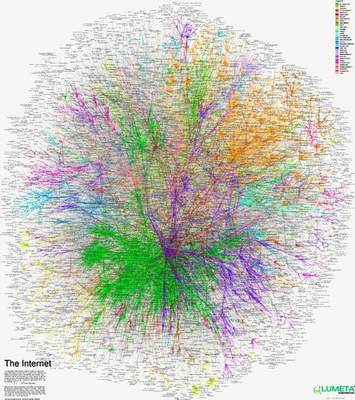Peta Internet, dibuat dengan visualisasi traceroute. Peta ini dibuat dari sebuah komputer di Bell Labs di New Jersey, ke 130000 host di Internet. Setiap titik ujung menunjukkan network lain, baik network kecil maupun network perusahaan besar; dan setiap titik temu menunjukkan router. Bell Labs juga menggambarkan apa yang terjadi pada network perusahaan yang mengalami merger dan sebagainya, termasuk juga network yang routingnya mengandung keanehan, baik yang disengaja maupun tidak. Cukup menarik. Konon gambar-gambar ini juga dijadikan poster dan dijual di http://www.peacockmaps.com/.
sekedar menjalankan tugas …
Di SD kita diajari tentang bilangan irasional, yaitu yang kalau didesimalkan membentuk deretan angka di belakang koma dengan panjang tak terhingga. Tapi setidaknya bilangan macam ini bisa ditulis singkat, misalnya 2½. Terus ada juga bilangan transendental, yang lebih irasional lagi ;), soalnya nggak bisa ditulis sederhana dengan bilangan rasional. Contoh yang khas adalah ? dan e. Naik ke SMP, kita dikenalkan dengan bilangan imajiner, yaitu i yang didefinisikan sebagai (-1)½.
Seorang matematikawan mencemooh seorang filsuf, yang konon bermain-main dengan wacana yang diciptakan memang untuk dipermainkan. Si filsuf membalas bahwa matematikawan juga hanya ahli mempermainkan seperangkat simbol yang memang diciptakan khusus untuk itu. Nggak ada yang ada di luar konteks, gitu katanya.
Tapi waktu kita beranjak ke SMA, masuklah sebuah teori konspirasi, heh. Ternyata si ?, e, dan i memiliki hubungan dalam formulasi ei? = -1. He-he :).
© 2025 Kuncoro++
Theme by Anders Noren — Up ↑
